系统GMM的工具变量怎么选择,高效优化策略解析

你有没有想过，在经济学研究中，如何选择合适的工具变量来估计系统广义矩估计（System GMM）模型，这可是个技术活儿呢！想象你就像是一位侦探，在茫茫数据海洋中寻找那些能帮你揭露真相的线索。今天，就让我带你一探究竟，看看系统GMM的工具变量怎么选！

一、何为系统GMM？

首先，得先弄明白什么是系统GMM。GMM，全称广义矩估计，是一种统计方法，用于估计线性或非线性模型的参数。而系统GMM，则是GMM的一种变体，特别适用于动态面板数据模型。它通过同时估计多个方程，来提高估计的效率和精度。

二、工具变量的重要性

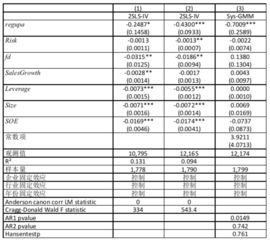
在系统GMM中，工具变量的选择至关重要。因为动态面板数据模型往往存在内生性问题，即模型中的解释变量与误差项相关。这时，工具变量就能帮我们解决这个难题。它就像是一把钥匙，能打开数据背后的真相。

三、选择工具变量的标准

那么，如何选择合适的工具变量呢？以下是一些关键标准：

1. 相关性：工具变量应该与内生解释变量高度相关，但与误差项不相关。这可以通过统计检验来验证。

2. 外生性：工具变量应该是外生的，即不受模型中其他变量的影响。

3. 可识别性：工具变量应该满足可识别性条件，即工具变量数量应大于内生解释变量的数量。

4. 一致性：工具变量应该是一致的，即在不同样本或不同时间点上，工具变量的选择应该保持一致。

四、常见工具变量的选择方法

1. 滞后变量：将内生解释变量的滞后项作为工具变量，这是一种最常用的方法。

2. 控制变量：选择与内生解释变量相关，但与误差项不相关的变量作为工具变量。

3. 工具变量组合：将多个工具变量组合起来，以提高估计的效率和精度。

4. 内生解释变量的外生部分：如果内生解释变量具有外生部分，则可以将其作为工具变量。

五、案例分析

为了更好地理解工具变量的选择，让我们来看一个实际案例。假设我们要研究某地区经济增长与固定资产投资之间的关系。由于固定资产投资可能受到政府政策的影响，因此存在内生性问题。我们可以选择以下工具变量：

1. 上一年度的固定资产投资额（滞后变量）。

2. 地区人均收入（控制变量）。

3. 地区人口增长率（控制变量）。

通过这些工具变量，我们可以估计出经济增长与固定资产投资之间的真实关系。

六、

选择合适的工具变量对于系统GMM模型的估计至关重要。通过遵循相关标准，并结合实际案例，我们可以找到那些能帮助我们揭示数据背后真相的工具变量。所以，下次当你面对一个复杂的动态面板数据模型时，不妨试试这些方法，相信你一定能找到那把打开真相之门的钥匙！